Ball-end milling cutters are essential tools in the CNC machining of complex and free-form surfaces. Their demand is significant, yet the manufacturing process remains challenging due to their intricate geometry. Most ball-end cutters are currently produced using multi-axis CNC machines, which are expensive (often costing millions of dollars), leading to high per-unit production costs. To address this issue, researchers began exploring non-numerical machining methods for ball-end mills as early as 1991. This approach aimed to reduce tooling costs by simplifying the machining process.
In collaboration with other researchers, a mathematical model was developed for both the rake face and flank face of the ball-end cutter. These models laid the foundation for serial production of such tools. Further research led to the use of planar curved profiles instead of space curves during the grinding of the flank face, significantly lowering the cost of tool production.
This paper aims to provide a comprehensive overview of the principles and methods behind non-numerical machining of ball-end milling cutters. It summarizes key concepts from existing literature and presents the core mathematical models that enable the creation of these complex cutting tools.
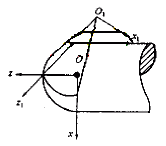
Fig.1 Principle of rake face machining
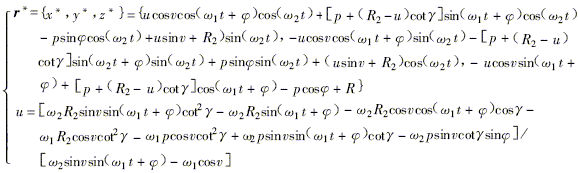
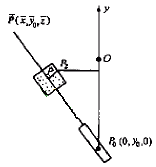
Figure 2 flank machining principle
Continuous Grain Powder Coating
Continuous grain powder coating
Continuous grain powder coating,net grain,Continuous grain
HLM Powder Coating CO,.Ltd , https://www.holymepowder.com